| Truncated tetraoctagonal tiling | |
|---|---|
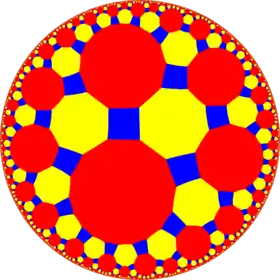 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 4.8.16 |
| Schläfli symbol | tr{8,4} or |
| Wythoff symbol | 2 8 4 | |
| Coxeter diagram | |
| Symmetry group | [8,4], (*842) |
| Dual | Order-4-8 kisrhombille tiling |
| Properties | Vertex-transitive |
In geometry, the truncated tetraoctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one octagon, and one hexakaidecagon on each vertex. It has Schläfli symbol of tr{8,4}.
Dual tiling
 |
 |
| The dual tiling is called an order-4-8 kisrhombille tiling, made as a complete bisection of the order-4 octagonal tiling, here with triangles are shown with alternating colors. This tiling represents the fundamental triangular domains of [8,4] (*842) symmetry. | |
Symmetry

There are 15 subgroups constructed from [8,4] by mirror removal and alternation. Mirrors can be removed if its branch orders are all even, and cuts neighboring branch orders in half. Removing two mirrors leaves a half-order gyration point where the removed mirrors met. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The subgroup index-8 group, [1+,8,1+,4,1+] (4242) is the commutator subgroup of [8,4].
A larger subgroup is constructed as [8,4*], index 8, as [8,4+], (4*4) with gyration points removed, becomes (*4444) or (*44), and another [8*,4], index 16 as [8+,4], (8*2) with gyration points removed as (*22222222) or (*28). And their direct subgroups [8,4*]+, [8*,4]+, subgroup indices 16 and 32 respectively, can be given in orbifold notation as (4444) and (22222222).
| Small index subgroups of [8,4] (*842) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | 1 | 2 | 4 | ||||||||
| Diagram |  |
 |
 |
 |
 |
 | |||||
| Coxeter | [8,4] |
[1+,8,4] |
[8,4,1+] |
[8,1+,4] |
[1+,8,4,1+] |
[8+,4+] | |||||
| Orbifold | *842 | *444 | *882 | *4222 | *4242 | 42× | |||||
| Semidirect subgroups | |||||||||||
| Diagram |  |
 |
 |
 |
 | ||||||
| Coxeter | [8,4+] |
[8+,4] |
[(8,4,2+)] |
[8,1+,4,1+] = |
[1+,8,1+,4] = | ||||||
| Orbifold | 4*4 | 8*2 | 2*42 | 2*44 | 4*22 | ||||||
| Direct subgroups | |||||||||||
| Index | 2 | 4 | 8 | ||||||||
| Diagram |  |
 |
 |
 |
 | ||||||
| Coxeter | [8,4]+ |
[8,4+]+ |
[8+,4]+ |
[8,1+,4]+ |
[8+,4+]+ = [1+,8,1+,4,1+] | ||||||
| Orbifold | 842 | 444 | 882 | 4222 | 4242 | ||||||
| Radical subgroups | |||||||||||
| Index | 8 | 16 | 32 | ||||||||
| Diagram |  |
 |
 |
 | |||||||
| Coxeter | [8,4*] |
[8*,4] |
[8,4*]+ |
[8*,4]+ | |||||||
| Orbifold | *4444 | *22222222 | 4444 | 22222222 | |||||||
Related polyhedra and tilings
From a Wythoff construction there are fourteen hyperbolic uniform tilings that can be based from the regular order-4 octagonal tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 7 forms with full [8,4] symmetry, and 7 with subsymmetry.
| Uniform octagonal/square tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [8,4], (*842) (with [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (*4222) index 2 subsymmetries) (And [(∞,4,∞,4)] (*4242) index 4 subsymmetry) | |||||||||||
= = = |
= |
= = = |
= |
= = |
= |
||||||
 |
 |
 |
 |
 |
 |
 | |||||
| {8,4} | t{8,4} |
r{8,4} | 2t{8,4}=t{4,8} | 2r{8,4}={4,8} | rr{8,4} | tr{8,4} | |||||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 | |||||
| V84 | V4.16.16 | V(4.8)2 | V8.8.8 | V48 | V4.4.4.8 | V4.8.16 | |||||
| Alternations | |||||||||||
| [1+,8,4] (*444) |
[8+,4] (8*2) |
[8,1+,4] (*4222) |
[8,4+] (4*4) |
[8,4,1+] (*882) |
[(8,4,2+)] (2*42) |
[8,4]+ (842) | |||||
= |
= |
= |
= |
= |
= |
||||||
 |
 |
 |
 |
 |
 |
 | |||||
| h{8,4} | s{8,4} | hr{8,4} | s{4,8} | h{4,8} | hrr{8,4} | sr{8,4} | |||||
| Alternation duals | |||||||||||
 |
 |
 |
 |
 |
|||||||
| V(4.4)4 | V3.(3.8)2 | V(4.4.4)2 | V(3.4)3 | V88 | V4.44 | V3.3.4.3.8 | |||||
| *n42 symmetry mutation of omnitruncated tilings: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | |
| Omnitruncated figure |
 4.8.4 |
 4.8.6 |
 4.8.8 |
 4.8.10 |
 4.8.12 |
 4.8.14 |
 4.8.16 |
 4.8.∞ |
| Omnitruncated duals |
 V4.8.4 |
 V4.8.6 |
 V4.8.8 |
 V4.8.10 |
 V4.8.12 |
 V4.8.14 |
 V4.8.16 |
 V4.8.∞ |
| *nn2 symmetry mutations of omnitruncated tilings: 4.2n.2n | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *nn2 [n,n] |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||||||||
| *222 [2,2] |
*332 [3,3] |
*442 [4,4] |
*552 [5,5] |
*662 [6,6] |
*772 [7,7] |
*882 [8,8]... |
*∞∞2 [∞,∞] | |||||||
| Figure |  |
 |
 |
 |
 |
 |
 |
 | ||||||
| Config. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | ||||||
| Dual |  |
 |
 |
 |
 |
 |
 |
 | ||||||
| Config. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | ||||||
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

